Random Genetic Drift -- The Breeder's Hidden Enemy

Copyright ©1999 J. Jeffrey Bragg

IF THERE IS one single concept that is crucial to our understanding of the situation in which the world of purebred dog breeders finds itself as the millennium turns over, I would think that concept must be random genetic drift. One hears the concept mentioned occasionally, yet I suspect that very few breeders really understand it thoroughly and correctly. Let us then try to explore this notion of random genetic drift. It is one of the fundamental theories of population genetics. In its full expansion it becomes rather complex mathematically, yet when reduced to its most basic form it is extremely simple and straightforward.

Population Size

TO BEGIN WITH, keep in mind that random genetic drift has its most powerful effect in small populations. What do we mean by “small” in this context? We mean those populations that are the furthest removed from infinite number. Consider bacteria: microscopic in size, present everywhere that the correct conditions of temperature, humidity, and pH exist, their populations probably number untold trillions or quadrillions – pretty close to infinite. On the other side of things, consider whooping cranes, condors and similar rare and endangered species of wild birds: the entire known populations of such species may number something like ten to fifty individuals. Purebred dog breeds, obviously, lie somewhere in between; but many of them are statistically much closer to the rare birds than they are to the bacteria. A glance at The Canadian Kennel Club's registration figures for a recently reported six-month period shows that, of the 160 breeds reported, 54 of those breeds registered 5 or fewer litters over the six-month reporting period. Even the most numerous breed, the Labrador Retriever, registered only 825 litters and 4,552 individual dogs over the same period. Obviously purebred dog populations are a far cry from infinite numbers. Genetic drift, then, will have its greatest influence on exactly such populations as those of our dogs.

The population size factor is more influential yet than it first appears, due to the way in which purebred dog populations are bred. In many breeds the effective breeding population is a great deal smaller than the actual population figures would suggest. Unless the number of males and females in the breeding population remains equal, the discrepancy between the number of males and females that actually contribute to the production of each generation will limit the effective breeding population. This limitation can be quite dramatic in breeds, such as the German Shepherd Dog, in which a limited number of very popular stud dogs account for a large proportion of the litters born to a large population of brood bitches. As a rule of thumb, the effective breeding population cannot exceed four times the number of sires in use. In the case of the GSD, a breed which surely must number in the hundreds of thousands of individual animals worldwide, the effective breeding population has been calculated to be something like six hundred, due to the persist overuse of popular stud dogs generation after generation.

The Nature of Mammalian Reproduction

OUR UNDERSTANDING of random genetic drift must begin with the nature of mammalian reproduction. We all know that it takes two mammals to make more mammals: specifically, a male (whom dog breeders call the sire) and a female (whom they call the dam). The sire contributes one sperm cell per puppy; the dam contributes one egg cell or ovum per puppy. On the level of individual genes, or equally on that of the chromosomes upon which genes are found, the basics remain the same: at each gene location or locus, an individual mammal has two copies of the gene belonging to that locus, one copy on each of two paired chromosomes – one chromosome (and one allele) from the sire and one from the dam. There may be more possible alleles (alternative versions of a single gene) than just two at any given locus, but no normal individual has more than two, one from each of the two paired chromosomes that carry that locus in the hereditary material (the DNA) of every cell in the animal's body. The two alleles may be identical (making the animal homozygous for that trait) or non-identical (making the animal heterozygous for that trait). Of the two gene copies that the sire possesses, he can contribute only one copy to each of his progeny; the same is true of the dam. Each parent gets one chance only to influence each genetic trait in each individual progeny, by contributing one gene at each locus, and thus every progeny has half its genetic heritage coming from its sire and half from its dam. Perhaps all this sounds as though I am elucidating what is already abundantly obvious to all of us, but we need to remind ourselves of these very basic facts, because what we have just described is a process of binomial sampling. Since the chromosomes and genes in the sperm and ova are created afresh from cells already present in the parent body, in such a way that the originals are not lost in the process and the total stock of gene “possibilities” is not diminished, it is actually a process of binomial sampling with replacement. This means that it's not like dealing out a deck of cards, in which everyone knows that once three aces have been dealt there can be only one ace remaining in the deck, so that the probabilities of a player receiving an ace change even as the cards are dealt out. By contrast, in the reproductive process the stock of genes is virtually infinite; the probabilities are not altered by the genes contained in ova or sperm already produced.

This means that gametic sampling, which is the correct term for the distribution to the progeny of the genes held by male and female, is a process closely analogous to that of flipping a coin to see if it lands “tails” or “heads.” That, too, is a process of binomial sampling with replacement, since there are only two possibilities and the probabilities at each toss remain unaltered by previous tosses. Let's emphasise that, because people sometimes assume intuitively that if you toss “heads” nine times running, you must have a 90 percent or better chance of tossing “tails” on the next throw. Wrong! No matter how many times you toss “heads” (providing the coin is a “fair coin” with no weighting to make it tend to fall one way more often than another), the probabilities on the next toss always remain fifty/fifty.

If you toss a fair coin one thousand times, you have every reason to expect that the final tally will be rather close to 500 heads and 500 tails. All right, you wouldn't be too surprised to see 507 heads and 493 tails, and the actual result would still be a good fit to the theoretical expectation of 500/500. Instead of 50%/50%, the actual results would then be 50.7%/49.3% – close enough to satisfy most of us.

But if you only tossed the coin ten times, the actual result could turn out to be 7 heads and 3 tails, which would not be a good fit at all to our theoretical expectation of 5/5, because percentage-wise it would be not 50%/50% but 70%/30%! The error involved in this example is called sampling error. It is a basic principle of random statistical sampling processes of this kind that the smaller the sample involved, the greater is the potential for deviation from the theoretically expected probabilities.

Up to this point everything I've explained has probably been quite obvious and by now you may well think I'm insulting your intelligence, but at this point when we stop talking about coin tossing and go back to sampling genes, important things start to happen which, although equally logical, are by no means quite so obvious to everyone.

Allele Frequency and How It Changes

POPULATION GENETICISTS speak of the allele frequency of a particular version of a gene at a given locus within a finite population. Let's create an imaginary example in which we have a population of ten dogs, five males and five females. We'll call the population number “N” (N = 10), and consider the gene locus “B” which we'll say influences the pigment colouring the noses of the dogs in that population and has two competing versions, upper-case “B” representing dominant black pigment and lower-case “b” representing recessive liver pigment. Since every individual has two copies of the B-locus gene, there will be a total of twenty copies of the nose-color gene (2N) in the total population. If there are 14 copies of version “B” and 6 copies of version “b” then geneticists say that the allele frequency (denoted by the letter F) of B = 0.7 and the allele frequency of b = 0.3. (The total must always add up to unity –1.0.) Notice that this measurement of allele frequency says nothing about how many dogs actually have black noses and how many have liver noses. It's possible that all ten dogs might have black noses; it's also possible that as many as three of them could have liver noses. That would depend upon the distribution of the two competing versions among the individual animals. In either case the allele frequency remains the same, since we are only talking about the total number of copies of each competing version within the entire population, not about how they are distributed among the individual dogs.

If there are just so many copies of each allele within the population, 14 copies of B and 6 of b, then it's reasonable to ask whether these proportions (0.7/0.3, or 70%/30%) are likely to change, and if so, what might cause such a change. In order to answer that, we must look briefly at a fundamental principle of population genetics, called the Hardy-Weinberg Principle. Among other things, this principle states that allele frequencies will remain stable within a population over successive generations provided that certain conditions exist. Among these preconditions for stable allele frequencies are: non-overlapping generations, random mating, very large population size, no “migration” (movement of individuals into or out of the population), and no selection pressure. None of those preconditions are met in purebred dog populations! So we have at least five factors present that are potentially capable of changing allele frequencies in our imaginary example, as well as in our purebred dog breed populations in the real world.

Of those factors for change, the most potent are small population size, non-random mating, and extreme artificial selection pressure. Small population size is the most basic, because it readily generates the kind of sampling error that we saw in the ten-time coin-tossing exercise. We saw that it was easy to wind up with a 7/3 result even though the probabilities were 50/50. In our example, however, the probabilities at the outset are 70/30 due to the greater abundance of copies of “B”. It is possible that the relative abundance of the two versions might remain the same from one generation to the next, but the same kind of random factors that influenced our small-sample coin toss could easily operate to make the relative allele frequencies of “B” and “b” change from 0.7/0.3 in the parental generation to 0.8/0.2 in the first filial generation, or they might operate in the other direction to change the frequencies to 0.6/0.4, too. Neither result would be difficult to imagine.

Then, when we bred the second filial generation, we would start from a new distribution of allele frequencies. The results, of course, would not be influenced by the previous draw in the genetic lottery any more than one toss of a coin is influenced by the previous one. One possibility is that the relative frequencies might move back to the original distribution. Another is that they would remain unchanged; or again, they might become yet more extreme, say 0.9/0.1, or 0.5/0.5. Already we can see two alternative scenarios emerging from this random binomial sampling process. In the first scenario, an allele that was only relatively uncommon gradually becomes really rare. In the second, the same relatively uncommon allele becomes more widely distributed. Let us suppose that in the third filial generation, the relative allele frequencies change yet again. If they were 0.9/0.1 in the second generation, then it would be quite possible that in the third generation they might become 1.0/0.0, in which case the minority allele would have disappeared completely from the population! If they were 0.5/0.5, they might easily become 0.4/0.6, in which case the allele which began as a minority presence of 30% would have progressed to a majority of 60%.

In the real world, of course, it is not likely that such extreme changes of allele frequency would occur in just three generations, but in such a small population it is definitely quite possible for the minority “b” allele with its initial frequency of 0.3 to become either lost (frequency 0.0) or fixed (frequency 1.0) within four to eight generations, solely through the operation of sampling error. Let's notice two things about this possibility. The first is that the breeding history of most purebred dog populations in a closed stud book already involves twenty to thirty or more canine generations. Many breeds have existed within the closed registries of The Canadian Kennel Club and The American Kennel Club for sixty to one hundred years or more; average generation times vary from two to six years. So there has already been plenty of time for alleles present in the original founder population to become either fixed (allele frequency = 1.0) or lost (allele frequency = 0.0) solely through the operation of sampling error.

The other thing to notice is that sampling error is not the only factor that can influence allele frequency. The way purebred dogs are bred almost invariably involves non-random mating and artificial selection. Random mating would imply that every male and female that survive to adulthood have more or less an equal chance of mating and making their contribution to the next generation In the purebred dog world this is far from being the case. Breeders consciously choose the sire and dam to produce each new litter. When a litter is born, the individuals from that litter that will ultimately produce the next generation are always carefully selected, and in their turn mates for them will be carefully chosen by the breeder. Thus each generation involves a fairly sharp cutback of the total available population to determine the actual breeding population.

Moreover, dog breeders vociferously insist that they select consistently for particular traits, generation after generation. In the case of show dog breeders, traits that are made the object of such selective breeding often turn out to be recessive traits genetically. In order for a fully recessive trait to be expressed in the phenotype, the actual physical expression of genes in an individual animal, that trait must be homozygous, that is to say, the individual must have two identical copies of the recessive gene. In the case of the nose-color gene we used for our example, only the dogs whose genotype is “bb” will have liver noses. The “Bb” heterozygotes will be black-nosed, as will the homozygous “BB” individuals. By this simple fact hangs a long and pregnant tale of dog-breeding!

Theoretical Breeding History of a Small Population

To get a clear idea of how such a change of allele frequency can happen, let's attempt to track a theoretical population's breeding history with reference to the B-locus. To keep things as simple as possible, we'll make some initial assumptions that will limit other variables. Assume that the breeding population consists of ten animals, that the animals in each generation are bred only once and then retired, that generations are separate and non-overlapping, and that from each filial generation another ten animals are selected for breeding.

In order to understand clearly what happens in the course of each generation's breeding and selection, we'll assume that we as observers know the actual genotype of every single animal, although the breeder herself cannot know the genotypes before selecting an animal or deciding upon a mating. We'll start with assumed allele frequencies of FB = 0.7, Fb = 0.3, and we'll assign genotypes to the individual animals as follows:

Notice that we have the correct number of each allele: 14 B and 6 b. Notice also that nine animals are black-nosed phenotype and only one is liver-nosed (bb). Now for the first filial generation the males in the top row will all be mated, each one to the female immediately below him in the bottom row. We'll just list the genotypes of the progeny in each litter:

Litter #1	Litter #2	Litter #3	Litter #4	Litter #5
(BB x Bb)	(BB x BB)	(Bb x Bb)	(BB x bb)	(Bb x BB)
BB (m)	__BB (m)__	BB (m)	__Bb (f)__	BB (m)
BB (f)	BB (f)	__bB (f)__	Bb (f)	bB (m)
Bb (m)	BB (f)	Bb (f)	__Bb (m)__	__BB (m)__
Bb (f)	__BB (f)__	__BB (m)__		bB (m)
__BB (m)__	BB (f)	bb (f - dies)		__BB (f)__
__Bb (f)__	BB (m)	BB (m)

We got three litters of six pups each, one of three pups, and one of five. Twenty-six puppies. Let's keep the math easy by assuming that the female bb puppy in Litter #3 was a weakling that died in the nest, leaving us with 25 pups, so that 2N = 50. We have fifty copies of the B-locus gene in the F1 generation; counting up the two alleles, we find B = 40 and b = 10 (since we are concerned with the gene frequency of the surviving F1 population, we don't count the dead puppy's gene copies). But wait! That means that FB = 0.8 and Fb = 0.2! Let's look back and make sure there was nothing unusual about any of those litters. Litter #1 has exactly the distribution of genotypes that we should expect from a mating of BB x Bb -- three BB individuals and three Bb's. Nothing wrong there. Litter #2 consists entirely of BB puppies, but both the sire and the dam were homozygous BB genotypes, so that was all they could possibly produce. The theoretical expectation of genotypes for Litter #3 would be equal numbers of BB, Bb, bB, and bb; in this case, we certainly did get one of each of those genotypes, but the litter consisted of six puppies not four, and the two additional pups both happened to be BB homozygotes. This is the only litter that is in any way unusual, but the actual genotype distribution is not far enough from the expectation to be really improbable. Chalk this one up to sampling error. Litter #4 consists of three pups of the only possible genotype for that mating, all Bb heterozygotes. Litter #5's theoretical expectation is half BB homozygotes and half bB heterozygotes; we got just that, but the odd-numbered puppy, the lone female, turned out to be another BB (she might just as easily have had the bB genotype as the probability was a toss-up).

Of the five litters in the first filial generation, only one is the slightest bit unusual, and it was not at all an improbable result, just a deviation from the expected distribution of the kind that any breeder who knows her colour genetics has seen time and time again over the course of her breeding career. All the same, the resulting population of twenty-five growing puppies has a gene frequency that is measurably different from that of the parental generation. Also notice that we no longer have any liver-nosed animals in this generation; there was one such pup but it happened to be the one that died. Of the twenty-five survivors, the breeder has no way of knowing, before she selects them for breeding, which are BB homozygotes and which are Bb or bB heterozygotes; they all have the black-nose phenotype, so we cannot know until they have been bred which carry the b recessive. Even then, the only way to identify the heterozygotes for certain would be to test-breed every individual to a homozygote bb partner. (This is why the notion of test-breeding to identify carriers of dangerous recessive genes is a rather impractical proposition -- if the recessive is really a defective gene, you must produce litter after litter of puppies, half of which will be homozygous recessives, just to identify the carriers. Test-breeding works, as long as you aren't bothered about the humane considerations of breeding large numbers of defective animals that must then be euthanised.)

Now our breeder will select a male and a female from each of the five litters to breed the next generation. She won't mate any brothers and sisters, but otherwise there won't be any particular plan or pattern to these matings. Remember now, she has no way to identify which are the dominant homozygotes and which are heterozygotes carrying the recessive b gene.

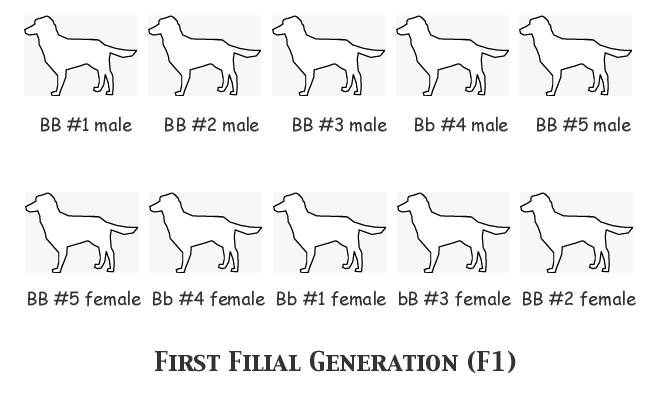
Note that the gene frequency of the group selected is no different from that of the entire F1 population; B = 16 copies and b = 4 copies. There was no way to ensure that the breeder's selective reduction of the breeding population from a potential twenty-five to a realistic ten wouldn't change the allele frequencies; she might have selected a population with a higher number of B copies and fewer b copies, or it could have been the other way 'round. She can only see the phenotype, not the genotype, so chance plays its part in the final result. In this case, though, I don't want the reader saying that I deliberately loaded the dice in selecting for this example, so I have made sure that the gene frequency of the selection is representative of the entire group.

Litter #6	Litter #7	Litter #8	Litter #9	Litter #10
(BB x BB)	(BB x Bb)	(BB x Bb)	(Bb x bB)	(BB x BB)
BB (m)	__BB (m)__	__BB (m)__	__BB (m)__	BB (m)
__BB (m)__	Bb (m)	BB (m)	Bb (f)	BB (m)
BB (m)	BB (m)	Bb (m)	bb (f)	BB (m)
BB (f)	Bb (f)	Bb (m)	__bB (f)__	__BB (f)__
__BB (f)__	BB (f)	BB (m)	Bb (f)	BB (f)
BB (f)	__Bb (f)__	__BB (m)__		__BB (f)__
BB (f)	BB (f)			BB (f)

This time mother nature threw the breeder a curve, as she experienced that not-uncommon and sometimes hoped-for phenomenon -- an all-male litter -- in the #8 mating. Since her plan has been to select two pups from each litter to carry on the breeding programme, she had to select two males from Litter #8 and compensate by taking two females from Litter #10. As luck would have it, she has unknowingly selected five BB genotype males! The lone liver-nosed female was not selected for breeding; she had a lot of competition in her litter and it may be that the breeder just liked one of the black-nosed heterozygote sisters better, we'll never know.

Litter #6	Litter #7	Litter #8	Litter #9	Litter #10
(BB x BB)	(BB x BB)	(BB x BB)	(BB x bB)	(BB x Bb)
BB (m)	__BB (m)__	BB (m)	__BB (m)__	BB (m)
__BB (m)__	BB (m)	__BB (m)__	Bb (m)	BB (m)
BB (m)	__BB (f)__	BB (f)	BB (m)	__Bb (m)__
BB (f)	BB (f)	BB (f)	Bb (m)	Bb (m)
__BB (f)__	BB (f)	BB (f)	__BB (f)__	Bb (f)
BB (f)	BB (f)	__BB (f)__	BB (f)	__BB (f)__

On we go to the third filial generation of this experimental breeding colony. This time we see five nice litters of six puppies each. Three of those litters could not produce anything but the BB genotype, since both parents were BB. The other two matings were both homozygote BB males to heterozygote bitches. Of those two, one conformed perfectly to theoretical expectations, while the other (#14) produced only two heterozygote puppies instead of the theoretical three. There is nothing in any way remarkable in any of these litters; yet the gene frequency has shifted again, such that this time the allele frequencies are FB = 0.9167, Fb = 0.0833. There are now so few carriers of the recessive b gene in this population -- five pups out of thirty -- that chance must now play an increasingly large part in what happens next.

From three of the five litters the breeder will inevitably pick BB males and females. In litter #14 there are equal numbers of BB and Bb males and the odds are even that she'll pick a homozygote; that is what happens in the event. In Litter #15 it's a similar situation, and this time by chance she picks a heterozygote male! (If by chance she had chosen another homozygote, the recessive b gene would have been lost in the next generation.) Litter #14 has only BB females, so that is what is chosen. In Litter #15 it's down to pick with one female of each genotype; as it happens, the BB girl gets chosen. The allele frequencies of the breeding population turn out to be FB = 0.95 and Fb = 0.05 (if the other female had been chosen the ratio would have been 90/10). It should be obvious that by this point there is really only one way the situation can ultimately turn out, but let's go ahead and tabulate the litters of the fourth filial generation.

Litter #16	Litter #17	Litter #18	Litter #19	Litter #20
(BB x BB)	(BB x BB)	(BB x BB)	(BB x BB)	(Bb x BB)
BB (m)	BB (m)	BB (m)	BB (m)	BB (m)
BB (m)	BB (m)	BB (m)	BB (m)	BB (m)
BB (m)	BB (m)	BB (f)	BB (f)	BB (m)
BB (f)	BB (m)	BB (f)	BB (f)	bB (f)
BB (f)	BB (m)	BB (f)	BB (f)	bB (f)
BB (f)		BB (f)	BB (f)
BB (f)		BB (f)

Out of thirty puppies in this generation, only two are heterozygotes. As sheer blind luck would have it, the recessive allele will not disappear with this generation, because it is certain that one of the two heterozygote females from Litter #20 must be chosen; yet the situation will not improve in the next generation, unless by chance there are both male and female heterozygotes in the litter bred from that female, and unless one of each is chosen to represent that litter. The odds are against that happening. So chances are the next generation will either repeat the situation shown in this F4 generation, or else the recessive will finally be lost.

I hope that the reader has paid some attention to the distribution of males and females in these twenty litters. Of a total of 118 puppies whelped, half were males and half were females, as one would expect in any large group of progeny. Obviously the theoretical expectation is 50/50 -- yet, as any experienced breeder well knows, the sex ratio in any particular litter can be anything at all. Indeed, this variability of the sex ratio in each litter, seen against the background of an iron-clad 50/50 expectation, is the strongest possible demonstration of the effect of sampling error in binomial sampling with replacement, when only small samples are taken. If so much variability can show up in individual litters with respect to the trait of male or female sex, then obviously we can expect errors just as great in other genetic traits, just as much in those we never notice as in those we track closely.

I have played quite fairly with the reader in this example, yet I have effectively demonstrated how, within a small breeding population such as might be maintained by almost any breeder, a recessive allele with an initial incidence of thirty percent can be lost from the population within five or six generations -- solely through the operation of genetic drift amplified by normal selection practices. It is important to realise that the recessive was actively selected against only once, if then -- when the breeder failed to choose the liver-nosed female in Litter #9; and in fact that pup may have been passed over for reasons that had nothing to do with the colour of her nose. What is significant is that in each generation ten animals were selected out of a population of twenty-five to thirty-two. There is nothing unusual about this level of selection; it would be normal in most small or medium-sized kennels. Yet all it takes is sampling error plus this level of selection -- not even selection directed at the B-locus trait, just undifferentiated selection -- to push the original 30% recessive into oblivion.

Obviously the example I have just set forth is not the only possible course that such a situation can take; things can conceivably go the other way. The fact that the gene eliminated was a recessive one has little significance unless we are talking about traits that are obvious to gross examination. It IS more difficult to lose a dominant gene that can readily be seen, simply because the whole process takes place in plain view, because every individual with a single copy of a dominant colour gene (for example) shows his possession of that gene in his phenotype. But if we are talking about traits that cannot be seen by the eye, then minority dominant genes disappear just as readily as recessives. I believe that this is what has actually happened in many purebred registered dog breeds: dominant genes have disappeared from small breeding populations through drift plus selection, selection that was directed towards recessive traits of appearance found desirable in the show ring, leaving those breeds with homozygous recessive genotypes for many of the "genetic defects" that show up with such alarming persistence in today's purebred dog populations.

The Reality of the B-Locus in an Actual Breed Population

LET'S PAUSE NOW for a moment while we relate our chosen example a little more closely to reality. The "B" and "b" alleles are in fact real genes. These genes influence the ability of the dog's body chemistry to synthesise a compound called tyrosine-melanin. A dog that cannot synthesise tyrosine-melanin will not have black pigment anywhere on its body. A homozygous liver-nosed "bb" individual may have dark-pigmented hair in its coat, but that pigment will be yellowish-red to reddish-brown in colour, not black. We called the B-locus a nose-colour gene only because that is where its effect is most obvious! The dominant "B" gene is the common, normal allele in the general population of Canis familiaris as a species. The recessive "b" is usually an uncommon rarity.

However, we frequently see the homozygous recessive "bb" in the show ring among some sleddog breeds. The most obvious example is the CKC/AKC Siberian Husky. "bb" dogs are called "coppers" or "reds" in that breed; these colours became popular in the show ring during the 1960s and subsequent decades. Originally they were quite scarce, an uncommon novelty. Today they are common. Unquestionably the relative allele frequency of "B" and "b" has changed over the years, or rather has been altered by the actions of breeders. There is no question of this change being anything other than a matter of fashion or fad. The breed standard of the Siberian Husky allows all colours and white; it states no preference for any particular colour. Therefore this change of allele frequency in the Siberian Husky has not been motivated by any desire to "improve the breed," despite the insistence of most breeders that such is the goal of their breeding programmes. In fact, we must consider that this particular change represents the encouragement of a metabolic defect! We said that the normal canine body chemisty is represented by the "BB" or "Bb" genotypes and in both cases the individual is capable of synthesising the tyrosine-melanin compound that allows black pigment in the hair coat and the skin. Since the "copper" Siberian with its recessive "bb" genotype is incapable of synthesising tyrosine-melanin, we could legitimately say that it is the victim of a metabolic disorder -- a "genetic defect." Of course, nobody calls this trait a genetic defect, simply because the copper coat which it expresses is a common and much-admired feature in the show ring!

There is a curious feature of the "bb" genotype that is neither well-known nor much discussed among Siberian Husky fanciers. Let's recall that the breed mythos of the Siberian Husky depicts the breed as a fast and enduring sleddog with a past history of many triumphant victories in dogsled racing. Let's also recall that the "b" allele is generally distributed among northern breeds; copper-coloured dogs are regularly seen among Alaskan Malamutes and Canadian Eskimo Dogs as well as Siberian Huskies. Siberian Huskies have regularly contributed to unregistered "Alaskan husky" racing sleddog bloodlines, so we can assume that the "b" allele is also present in that genome. Nevertheless, this author recently observed the premier speed racing event of the entire North American continent, the Open North American Championship races in Fairbanks, Alaska, where the elite of "world-class Alaskan husky" racing sleddogs gather to decide the fastest team over a grueling race in the March sunshine of twenty miles the first day, twenty miles the second day, and thirty miles the last day, using teams which typically vary from fourteen to twenty-two dogs running at speeds of an average 17.5 to over 20 miles per hour. One surprising fact became obvious at that 1998 running of the ONAC: out of more than twenty teams involving well over three hundred top-flight racing sleddogs, there was not one single "bb" dog to be seen!

If the "bb" genotype has become common and generally accepted within the Siberian Husky show dog population, yet is virtually absent among the elite of high-speed dogsled racing, the conclusion must be drawn that the homozygous recessive of the B-locus gene has metabolic effects that go beyond restriction of black pigment in the coat and skin, effects that decrease overall metabolic efficiency of the dog with respect to its capacity to demonstrate sustained racing speed over a twenty- to thirty-mile race course.

(I do not claim that "bb" genotype sleddogs are all totally incapable of racing. Here and there an individual can be found that is apparently able to participate in a competitive racing team. Nevertheless these individuals are extremely uncommon, compared to the frequency of their appearance in the Siberian Husky show dog population. It is difficult to escape the conclusion that in some way the homozygous "bb" genotype represents a metabolic liability to the dog, whether directly through the action of the homozygote genotype, or through some other gene that has been influenced by the selection process that gave rise to the "bb" homozygote.)

The Problem of Gene Linkage

THIS LAST POSSIBILITY must be examined closely, because it relates intimately to the inadvertent damage that I believe is often done by show dog breeders' selection for homozygous recessive traits of superficial appearance. Our example of the B-locus may or may not be an instance of direct genetic damage through such selection, of consciously selecting for a trait that turns out to be harmful to the physiological well-being of the dog. More significant, I think, is the possibility that, in the course of selecting for homozygous recessive traits of appearance, other beneficial genes are lost or other harmful genes are fixed.

How could these things occur? Quite simply, I think. We must not forget that the units that we call "genes" are not simple, single discrete entities. The usual popular understanding of practical genetics has led everyone to think of them in that way. Nevertheless, nobody has ever seen a "gene" as such. Scientists, when pressed to define what is meant by a gene, will usually confess that this is a convenient conceptualisation that doesn't conform too closely with the biochemical reality of cell structures. There is no structure within a cell that can be identified as a single gene! There is only genetic material, consisting of DNA strands that are found in several locations, but most importantly in the chromosomes of the cell nucleus. Chromosomes are not even visible most of the time. They become apparent during the process of cell division. It is certain that the bulk of what we refer to as genes occur on the chromosomes. However, a canine cell is said to possess 78 chromosomes. The number of individual "genes" in the canine genome (the sum total of the dog's genetic material) is thought to be on the order of one hundred thousand or more. It is important to realise that this number is only an estimate. The exact number of genes in the dog species is not known. Perhaps it cannot be known with any certainty, because it is difficult to determine the exact nature of a gene. One gene may control more than one trait, or conversely, a single trait may be influenced by a constellation of genes. The exact and particular nature of a gene defies definition.

Given the foregoing situation, it is absolute lunacy for a breeder to assume that he can selectively deal with individual genes in isolation. When gametogenesis takes place (the process by which the dog's reproductive organs generate spermatozoa or ova), the chromosomes within the nuclear material separate and divide. An individual dog possesses 39 pairs of chromosomes, each pair representing one chromosome from its sire and one from its dam. That dog, as a parent, can pass on only one member of each pair to each of its progeny. It can pass on the chromosome from its own sire, or the one from its dam, but not both. (In some cases, which we'll examine more closely below, the chromosome it passes on can be partly from one parent and partly from the other, but this is the exception, not the rule. In any normal case, any given DNA sequence passed on by a parent will come either from its sire or its dam but never from both.)

Typically, then, the smallest unit of selection that can be dealt with in any given mating is not an individual gene, but the chromosome upon which that gene happens to be found! This is of the utmost importance, yet one almost never hears this fact mentioned. No matter, anytime a breeder selects a parent animal with reference to a particular trait, he is not selecting just for that trait -- he is selecting for every single trait located on the same chromosome as the gene controlling the target trait. (Really, along with that he must accept that he is also selecting for all the other traits exemplified in that particular parent, plus those that are genetically present but not visible or expressed.) If he does not like some other trait on another chromosome of that parent (and remember that he has no direct perception of the location of the individual "genes" or of which chromosome they may be found on), he can always hope to select from among the progeny of the mating an individual that expresses the contribution of the other parent more strongly.

It is possible, through selection, to separate chromosomes from one parent or the other. It is much less possible to separate out individual genes located on the same chromosome. All the genes found on the same chromosome are effectively "linked." To separate them is feasible only if a process called crossing over happens to have occurred opportunely. Sometimes, in the course of separation and division of chromosomes within the cell nucleus, the two chromosomes of a pair become entangled in such a manner that, when they separate, the two resultant bodies are spliced versions with part of their length from one chromosome of the pair and part from the other. The probability that a given gene will thus become unlinked from the other genes on its chromosome of origin depends entirely upon its position on the chromosome. If it is located near either end of the chromosome, there is little probability of the gene becoming unlinked from the others through crossing over; if it is located near the midpoint, the probability is highest. There is no way, short of meticulous and indirect laboratory methods, for anyone to determine the probability that one gene will become unlinked from another gene on the same chromosome, nor even to determine readily that this has actually taken place.

I must apologise to the reader if the foregoing discussion has left her confused. The actual machinery of genes and chromosomes is still incompletely understood; it is still quite difficult to relate the reality of DNA sequences to the expression of visible or measurable traits in individual animals. These uncertainties are quite frustrating to the dog breeder who seeks a practical understanding of genetics as it relates to breeding and selection. Yet I think it is important to understand what we do not know, and what cannot readily be done or known, especially when we look at the selection process. If we imagine individual genes as being the size of garden peas, we should like to have some means of picking them out and moving them around that would be the size and accuracy of a pair of tweezers; whereas in reality, the selection tool at our disposal would be more like the bucket of a front-end loader! If we think to use such a tool to select a single gene and leave the others undisturbed, we are self-deceived. There is simply no way that the breeder can deal with single traits in isolation.

This is particularly true of homozygous recessive traits. The only way to achieve homozygosity where it is not already the case is through inbreeding and selection. Inbreeding is certain to influence many traits other than the target trait. Think about it: if, in order to achieve expression of one recessive gene, one must necessarily eliminate the other allele, is it not virtually inevitable that in the process of eliminating one dominant allele, other genes, particularly those located on the same chromosome, are bound to be eliminated as well? Other genes, as well as the desired recessive, fixed? Genes the exact nature and effects of which the breeder may remain totally ignorant? Think, too, about this: selection for a recessive trait quite frequently involves selecting just one individual for future breeding out of a litter; every time two parents produce one progeny that turns out to be the sole representative of those parents in future breeding, the gross amount of genetic diversity in that line is cut in half, because one individual can have only half the available genetic material from each parent!

Genetic Drift and the Closed Stud Book Breed Registry System

DOES THE READER now begin to comprehend the probable extent of genetic depauperisation inherent in the modern system of dog breeding and purebred registration? For as long as we continue to use the current system of registration, inbreeding and artificial selection, it is inevitable that the overall loss of genetic diversity will be sustained and significant. If the loss of genetic material cannot be stopped, then there is only other effective remedy possible -- and that is periodically to replace the lost material!

Yet consider further: the major umbrella registry organisations, CKC and AKC, operate under a completely closed stud book system. They make no provision whatever for periodic addition of new genetic material to the breeds they register. In every case, candidates for CKC and AKC registration are expected to descend from the original foundation stock of the breed in question -- one hundred percent. Oh, yes, the major kennel clubs accept imports from each other's stud books and from those of (some!) FCI countries -- but always on the understanding that the imports descend exclusively from the original breed foundation stock in all pedigree lines. Breeders of purebred AKC and CKC dogs apparently consider that "breed purity" is paramount, more important than genetic health, species soundness, or good temperament.

Most equine breed associations and other domestic livestock registries have "grading-up" provisions, whereby a purebred may be mated with a non-purebred and the progeny be registered (for example) as "half-Arab", a half-bred mated with a purebred to produce a "three-quarter-Arab", and the three-quarter-bred mated with a purebred to produce -- purebred Arab horse progeny! The Animal Pedigree Act 1988 of Canada provides that in order to be considered legally purebred, an animal must be at least seven-eighths descended from the original foundation stock of its breed, meaning that the grading-up process is enshrined in Canadian agricultural law, guaranteeing purebred status to progeny of three-quarter-bred and purebred parents. Yet The Canadian Kennel Club persists in requiring one hundred percent descent from original foundation stock, thereby ensuring that no breed in its stud book can ever be genetically refreshed. No provision whatever is made for new genetic input to existing breeds. The Club justifies its position by referring to the "integrity of its stud book" and the "reliability of its records" (despite the fact that it has only a much-abused "honour system" to ensure that parentage is correctly reported).

The closed stud book "breed purity" system has one undeniable major result: it is that, as long as this system remains in effect, the operation of genetic drift (and of other factors that accelerate the effects of genetic drift) can never be undone or counteracted. The net result is that each generation of AKC and CKC purebred dogs born has less genetic diversity. An inexorable tendency toward genetic impoverishment is build into the national all-bred canine registries. Presumably the ideal is for every purebred dog breed to become homozygous recessive at every possible locus, with a net genetic diversity of zero; for each individual of a breed to be a genetic laser-copy of whatever reigning show dog stud is deemed to be the living representative of the breed standard; for every dog breed to be like the cheetah, genetically depauperate, with a single homozygous genetic blueprint completely shorn of diversity, utterly vulnerable to the least change in its environment, having no possible response to new diseases, pollutants or other threats.

We are already halfway there! In many breeds it is common for the inbreeding coefficient in many litters to be on the order of fifty percent. That means the probability that any given gene received from the sire of a litter is identical by descent with the corresponding gene received from the dam is fifty-fifty -- a tossup! Every other gene is homozygous! That means half the original genetic diversity has already been eliminated from AKC and CKC dog breeds since they first began to be registered. To eliminate another half is not likely to take another hundred years, though. The effects of this breeding/registry system are cumulative; the net loss of genetic diversity probably rises on a skew curve. For many breeds it may already be too late. Random genetic drift, accelerated by sustained inbreeding and a high level of artificial selection for superficial traits, has already fixed in a homozygous state many harmful genes that in a natural, wild canid population would rarely if ever occur in such a state. Evidence that this is true is seen in the alarming upsurge in genetic diseases that have become a major concern in today's purebred dog community. Dog breeders, in their quest for exquisite breed type and absolute breed purity, have stripped their animals of the genetic diversity with which nature originally equipped the dog for his health and hardiness and as insurance against new environmental threats. How ironic it is that now, at the turn of the millennium, when all humanity are declared to be brothers regardless of race, when on every side all living creatures are most threatened by new virus diseases, widespread environmental pollutants, increased solar radiation, decreased oxygen supply, etc., those who profess love for their dogs insist upon depriving them of the genetic diversity they so badly require, and all in the name of a racist ideal which, if it were suggested in a human context, would be universally condemned.